Des conséquences économiques de la téléportation sur les coûts de transport

Voilà très longtemps que je n’ai pas fait un billet sur les dimensions économiques que l’on peut relever dans les œuvres cinématographiques, parfois présentes de manière explicite, mais le plus souvent de manière totalement inconsciente dans l'esprit des scénaristes, seul mon esprit tordu ayant sans doute l'idée de les mettre en lumière...

[Certains lecteurs pensent alors fortement que c'est surtout du au fait qu'il n'y a que moi que cela intéresse ! Mais alors, quel paradoxe, car, lecteur, si tu en es arrivé à ce point, c'est que tu me lis et donc que tu es intéressé !]

J’ai revu récemment un des chefs d’œuvre du cinéma fantastique,  "la mouche",, dans la version réalisée par David Cronenberg avec Jeff Goldblum, remake d'un classique des années 50 tout aussi bon, et un certain nombre de considérations économiques évoquées dans le film m’ont amusées. C'est l'objet de ce billet.

L’histoire est assez simple à résumer en quelques mots : un inventeur génial, physicien de son état, met au point un système permettant de téléporter d’abord de la matière inerte, puis, butant sur le problème de la téléportation des êtres vivants, trouve la solution, l’expérimente sur lui-même, ce qui causera sa fin. Au début du film, le scientifique dialogue avec la journaliste scientifique incarnée par Geena Davis et lui déclare la chose suivante pour la persuader d’écrire un livre qui relate sa découverte :

« Ce sera un livre sur l’invention qui a mis fin à tous les concepts sur les transports, les limites du temps et de l’espace ».

C’est là où j’ai bisqué.
En fait, cette idée renvoie au bon sens que nous avons tous et qui consiste à considérer que le problème du transport de biens ou de personnes est avant tout un problème de distance. Si la distance était abolie, au moyen d’un dispositif comme la téléportation, alors plus de problème de transport et un coût du transport nul ou quasi insignifiant.

Cela sonnerait-il le glas d’une discipline qui m’est chère, l’économie des transports, réduite à figurer au panthéon de l’histoire de la pensée, dans les oubliettes poussiéreuses réservées aux idées qui n’ont plus aucun intérêt, à l’instar par exemple de la théorie de la valeur marxiste ou de l’écrasante majorité des ouvrages de Bernard Henry-Levy ?

Précisément, rien n’est moins faux si on regarde la manière dont le problème du transport, notamment de personnes, est abordée dans la théorie économique moderne.

Les choses peuvent être comprises de manière intuitive : le problème du transport n’est pas seulement un problème de distance consistant à aller d’un point A à un point B, c’est aussi un problème de capacité de l’infrastructure qui permet de véhiculer choses ou êtres.  Ce problème de capacité n’est pas du tout vu par le film, qui a d’autres chats, ou plutôt mouches, à fouetter et là n’est pas son propos essentiel.

Toutefois, ceci est un point central. Tirons le fil lié à la découverte révolutionnaire de Brundle, l’inventeur malheureux de la téléportation incarné par Goldblum. Imaginons que son dispositif devienne parfaitement fiable, et se généralise au point de rendre obsolètes toutes les infrastructures de transport, terrestres, maritimes, aériennes, etc. Le système de Brundle implique l’accès d’une personne à un télépod localisé en A, le transfert de cette personne vers un autre télépod localisé en B. Le point crucial est qu’il n’est possible de téléporter qu’un objet ou être vivant à la fois, c’est d’ailleurs la source de la malédiction de notre génial inventeur, la procédure durant quelques secondes, et le temps de transport total n’étant pas lié à la distance entre A et B, puisqu’il s’agit précisément de téléportation.

Il n’en reste pas moins que le système implique un goulot d’étranglement. Difficile d’envisager de construire autant de télépods (ceux-ci sont coûteux d’un simple point de vue économique) que de personnes souhaitant se déplacer, et,  par conséquent,  le système a une limite de capacité. Par exemple, cette limite pourrait être par exemple, de 60 déplacements par heure par télépod, en supposant le temps d’entrée et de sortie total égal à une minute.

Or, qui dit limite de capacité dit congestion potentielle,  i.e. la possibilité d’avoir des coûts de transport non liés à la distance qui croissent en fonction de la demande de déplacement à un moment donné et en fonction du stock des déplacements restant à écouler au moment où je me présente devant le télépod. En effet, la congestion est un phénomène dynamique, qui implique un mécanisme de file d’attente, et par conséquent le temps de transport au moment m (ou le coût si je suppose négligeables les coûts financiers du déplacement dans un premier temps) croît en raison du total des déplacements restant à écouler, produit de la demande de déplacements pour les moments m-1, m-2, etc, précédents ainsi que de la demande instantanée en m. Le problème va être précisément qu’il n’est possible de transférer qu’une personne par minute…

Cette manière de concevoir le problème des déplacements de personnes et la formation de la congestion de manière dynamique a été proposée par William Vickrey en 1969 et formalisée par Richard Arnott, André de Palma et Robin Lindsey à la fin des années 80 dans ce qu’on appelle désormais les modèles de goulot d’étranglement (« bottleneck models »). Il faut bien dire que ces modèles, qui s'inspirent de la physique et de la recherche opérationnelle, ont constitué une véritable révolution dans le domaine de l’économie urbaine et de l’économie des transports.
Initialement, ces modèles cherchent à expliquer la formation de la congestion dans le cadre des déplacements quotidiens domicile travail en milieu urbain, en particulier les phénomènes de pointe du matin et du soir. Dans la configuration théorique la plus simple, tout le monde veut arriver au même endroit en même temps, on suppose des automobilistes homogènes, tous localisés au même endroit, et devant passer par le même itinéraire pour arriver par exemple dans le centre ville où sont localisés tous les emplois. Cet itinéraire a une certaine capacité d’écoulement par période de temps, par exemple 100 véhicules par minute. Les automobilistes doivent choisir simplement à quel moment partir de leur domicile sachant qu’ils doivent arriver à un moment précis, le même pour tous, et que leur coût de transport est constitué que du temps qu’ils passeront dans le goulot d’étranglement mais aussi du coût d’opportunité du temps lié au fait qu’ils peuvent arriver en avance ou en retard sur leur lieu de travail. Il y a donc un réel arbitrage à faire pour l’usager : soit je pars très tôt, je passe facilement le goulot car il n’y a pas grand monde, mais j’arrive en avance. Soit je pars très tard, au moment où il y a plus de monde, je subis le temps perdu dans le bouchon, et je risque en plus d’arriver en retard.

La congestion se forme bien de manière dynamique : tant que la demande instantanée est inférieure ou égale à la capacité du goulot, le temps d’attente (ou de passage du goulot) est nul. Toutefois, dès que la demande instantanée devient supérieure à la capacité, la congestion commence à se former et les véhicules s’accumulent dans une file d’attente, et il devient de plus en plus long d’arriver à passer le goulot. Puis, le nombre des départs instantané baisse, et la congestion finit par se résorber. La règle à l’intérieur du goulot est bien sûr premier arrivé –premier servi.

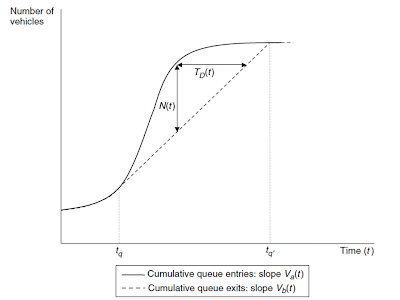
Le graphique ci-dessous, tiré de l’excellent livre de Ken Small et Eric Verhoef sur l’économie des transports urbains, illustre le modèle et la formation de la congestion :

Source : Small and Verhoef (2007), The Economics of Urban Transportation, Routledge.

Sur ce graphique, la valeur de N(t) représente l'écart entre la capacité cumulée au cours du temps (la droite en pointillés) et la demande cumulée à partir du moment où le nombre de départs devient supérieur à la capacité d'écoulement de la route (la courbe en traits pleins). La valeur horizontale T(t) correspond au temps passé dans le goulot pour un usager partant en t.

Il est même possible de simplifier encore le modèle, en supposant qu’un véhicule qui accède au goulot passe immédiatement si la capacité en t reste supérieure au stock de demande à écouler en t, puisque ce n’est pas un élément important en fait.

Il y a quelques années (désolé, je vais encore parler de moi comme dans le dernier billet), j’ai réalisé avec quelques collègues une série d’études expérimentales sur ce modèle (une référence ici), simplifié certes à outrance dans un cadre d’expérience de laboratoire, mais dont les résultats furent assez édifiants.  Même avec un petit nombre de joueurs dans ce jeu de goulot d’étranglement, on observe la congestion de manière systématique, ce qui signifie que les participants n’arrivent pas à  se coordonner suffisamment bien pour résoudre le problème de congestion, par exemple, le joueur 1 partant à l’heure 1, le joueur 2à l’heure 2, etc, ce qui minimiserait le coût total de transport, et l’efficacité serait de 100%. Dans nos expériences, le taux moyen d’efficacité tourne autour de 60%, ce qui est lié à la congestion.  Par ailleurs les résultats observés en laboratoire sont assez proches des prédictions théoriques issues du modèle de goulot d’étranglement.

Plus récemment, l’American Economic Review a publié une étude expérimentale de Daniel, Gishes et Rapoport en 2009 sur une version plus sophistiquée de ce modèle de goulot, basée sur l’idée de bottlenecks qui s’emboitent dans un grand bottleneck (pour parler simplement, deux petites routes qui se connectent sur une grande route). Les auteurs testent l’impact d’une augmentation de la capacité d’une petite route en amont, toutes choses égales par ailleurs, sur les coûts de transport. Ils observent en laboratoire une forme de paradoxe de Braess (phénomène dont j’avais parlé ici ), qui fait que l’augmentation de la capacité débouche de manière contre-intuitive sur une augmentation des coûts totaux des déplacements.
Pour en revenir au film de Cronenberg, et pour faire le lien avec ce qui vient d’être dit, même avec la téléportation généralisée, il n’est pas sûr que l’augmentation de la capacité en télépods permette de résoudre définitivement le problème des coûts de déplacement si un phénomène du type Braess se produit (pour qu’il se produise, il suffit que l’augmentation de capacité ne soit pas trop forte). Comme quoi une innovation technologique, même révolutionnaire, ne sonne pas la fin de nos réflexions dans le domaine de l’économie des transports, et qu’au contraire, elle les stimule sans doute.

J’en suis arrivé à la conclusion que la projection du film la Mouche serait une magnifique introduction à un cours moderne d’économie des transports, en supposant toutefois que la plupart des étudiants n’aient pas rendu leur déjeuner ou leur goûter à l’issue de la projection - le film est assez gore par moments quand même - , faute de quoi, même avec du talent, il sera difficile de leur demander un effort intellectuel...

Faire le bien ou éviter de faire le mal ? Quelques enseignements des expériences en économie

Au hasard de mes pérégrinations intellectuelles assez ardues de ces derniers mois, je suis tombé sur un article de Messer et al 2007 sur l'importance des effets de contexte dans le comportement de contribution au bien public. Comme tu le sais certainement lecteur, les économistes désignent par bien public un bien qui possède deux caractéristiques, la première étant l'indivisibilité d'usage (je peux utiliser le bien sans que cette utilisation ne gêne ou ne limite l'utilisation par un autre individu) et la seconde étant l'impossibilité d'exclure des utilisateurs potentiels (je ne peux empêcher mon voisin de profiter de l'éclairage public même s'il n'y contribue en rien parce qu'il fraude fiscalement par exemple)...

[C'est une image, mes voisins sont des gens très bien au-dessus de tout soupçon. J’espère qu’aucun percepteur zélé ne lit ces lignes]

Le problème avec les biens publics est la possibilité que les individus se comportent comme des passagers clandestins, c'est-à-dire qu'ils ne contribuent pas personnellement au bien public, la contribution étant généralement coûteuse et, du fait de ses caractéristiques d'impossibilité d'exclusion ,soiten tentés d'attendre un effort des autres sans le produire eux-même. Cette possibilité de free riding avait été évoquée par Knut Wicksell, un économiste autrichien, dès la fin du 19ème siècle.

Les études expérimentales sur cette question ont été extrêmement nombreuses et tendent toutes à montrer que le comportement de passager clandestin n'est pas aussi fréquent que cela, et qu'une petite proportion des individus sont réellement des passagers clandestins. Le problème est que cette petite minorité est relativement "toxique" car les individus qui ne sont pas des passagers clandestins de manière intrinsèque vont avoir tendance, si la contribution au bien public est répétée dans le temps, à punir les passagers clandestins en réduisant eux-même leur effort ou contribution au bien public (Voir Falk, Fehr et Fischbacher en 2005, Econometrica, pour plus de détails sur ce résultat.)

Bon, ce résumé très rapide (cette question a été abordée à de multiples reprises dans ce blog) n'est là que pour mettre en scène le sujet que je veux aborder, à savoir l'importance de l'effet de contexte ou de présentation dans les phénomènes de contribution au bien public.

L'effet de contexte, bien connu en économie expérimentale, a été mis en évidence par Kahneman et Tversky il y a bien longtemps (pour une description pédagogique , je te renvoie ici lecteur) : en quelques mots, il dit que les choix économiques sont sensibles à la manière dont les choix sont présentés. (dans le jargon des économistes, on dit qu'il y a un axiome (rarement explicitement posé d'ailleurs) d'invariance de description). Un nombre d'études considérables a mis en évidence cet effet dans le cas de choix individuels, mais peu l'ont fait dans le cas de choix impliquant ce que les économistes appellent un dilemme social, c'est à dire une situation dans laquelle la coopération entre individus serait souhaitable (tous contribuer au bien public) pour la communauté mais dans laquelle la rationalité va pousser les individus vers une issue d'équilibre moins bonne du point de vue de l'intérêt général.

L'étude de Messer porte précisément sur ce problème. L'exemple donné est celui de la donation d'organes.  Le don d'organes est typiquement un bien public. En effet, deux grands types de réglementations existent au niveau international. Dans le premier type, vous êtes supposés donneurs par défaut (si vous ne dites rien, on pourra utiliser votre corps pour des greffes ou autres) et dans le second type, vous êtes supposés non-donneur par défaut (il faut dire explicitement que vous souhaitez donner vos organes pour qu'ils puissent être utilisés pour des greffes).

Une étude de 2003 de Johnston et Goldstein parue dans la revue Science (« do defaults save lives? ») montre que les pays dans lesquels le statu quo pour la donation d’organes est le consentement (par défaut vous êtes donneur et vous devez indiquer à vos proches de manière explicite si vous refusez de donner vos organes) ont un taux de donation de 85.9% à 99.9%, tandis que pour les pays dans lesquels le statu quo consiste en un non consentement (la France jusqu’à une date récente), le taux de donation s’échelonnait entre 4.3% et 27.5%.

D’autres exemples sont possibles : en ce qui concerne par exemple la qualité de notre environnement, au sens écologique, vaut-il mieux mettre en œuvre des incitations permettant de créer du bien public, via des actions positives de dépollution, ou des incitations permettant d’éviter le mal public issu de comportements pollueurs ?

Dans le cadre des politiques de lutte contre l’effet de serre, la question se pose. Par exemple, dans un rapport du Centre d’Analyse Stratégique récent (consultable ici), à propos de la politique de lutte contre l’effet de serre, on peut lire qu’un des apports de l’accord de Copenhague, décrit généralement comme un échec, a été la mise en place de mécanismes (REDD+) qui visent à la fois à préserver la qualité de l’environnement mais également à mettre en œuvre des actions permettant d’en améliorer la qualité. En particulier, on peut lire ceci :

« L’Accord inscrit explicitement la mise en place d’un mécanisme dit « REDD + » visant à lutter contre la déforestation et la dégradation mais également à favoriser les plantations, la gestion forestière et la conservation des stocks de carbone »

Sous-entendu, il est bien de se soucier de préservation de l’environnement, mais sans doute faut-il faire en sorte que des actions plus volontaristes soient mises en œuvre.

La théorie économique est a priori neutre de ce point de vue : selon la théorie microéconomique, le contexte n’importe pas (voir ce qui a été dit précédemment) et l’efficacité des incitations dans un cas (création de biens publics) doit être la même que dans l’autre cas (limiter l’apparition de mal public).

C’est précisement l’objet de l’article écrit en collaboration avec Douadia Bougherara, de l’INRA, et David Masclet, bientôt publié dans une revue internationale, et dans lequel nous cherchons à mettre en évidence un éventuel effet de contexte dans le cas de biens publics. L’idée de départ est extrêmement simple : comparer un contexte de création de bien public à un contexte de préservation du bien public, ce dans le cadre d’une expérience d’assez grande envergure.

Pour le contexte de préservation, supposons que toutes les ressources des individus soient d’ores et déjà placées dans un pot commun (le bien public) et que le maintien de ces ressources dans le pot commun a un coût d’opportunité privé pour chaque agent. En retirant une unité du pot commun, il renonce à ce qu’il retirait de cette unité du bien collectif, mais peut utiliser cette ressource pour une consommation privée. Bien évidemment, en faisant là, puisqu’il s’agit d’un bien public, il créée une externalité négative car il détruit aussi l’utilité retirée par les autres membres de son groupe par rapport à cette unité qui était placée dans le bien public.

Pour le contexte de création, c’est plus simple. Chaque individu est doté d’une certaine quantité de ressources, et chacun d’entre eux doit simplement décider du montant qu’il investit dans le pot commun, ce montant investi ayant un coût d’opportunité privé (la consommation privée que l’agent ne pourra effectuer), mais génère une utilité issue de la consommation du bien public, ainsi qu’une externalité positive, puisque les autres membres du groupe profitent également des ressources mises dans le pot commun. C’est le fameux jeu de VCM (Voluntary Contribution Mechanism) utilisé la première fois par Isaac et Walker en 1988.

Pour tout dire, il existait déjà un article de James Andreoni écrit sur le thème, en 1995 mettant en œuvre à peu près exactement le protocole expérimentale que je viens de décrire et comparant le contexte de création et le contexte de préservation. Il arrivait à un résultat toutefois surprenant : le niveau de coopération était plus élevé en moyenne dans le contexte de création du bien public que dans le contexte de préservation. Le montant investi dans le contexte où chaque sujet devait investir dans le pot commun inexistant au départ était plus important que le montant retiré du pot commun préexistant au départ. Comme le notait Andreoni, et autrement dit, les sujets préféraient faire le bien que d’éviter de faire le mal (il écrit exactement « it must be that people enjoy doing a good deed more than they enjoy not doing a bad deed »).

Dans l’article que nous avons écrit, nous avons testé la robustesse de ce résultat. Il faut dire qu’il nous semblait assez incroyable et nous avions quelques doutes sur sa solidité : comment les individus pouvaient-ils être plus disposés à détruire le bien public qu’à le créer ? Cela nous semblait plus naturel de penser que, une fois le bien public crée, une forme de biais de statu quo ou de biais de dotation serait mis en œuvre, et que les participants auraient plus de facilité à préserver le bien public qu’à le créer. En effet, c’est précisément ce que suggère le biais de statu quo mis en évidence par Thaler en 1980. Si on donne un bien quelconque aux individus, ceux-ci sont prêts à faire plus d’effort pour le conserver que si on leur demande de faire des efforts pour obtenir ce même bien.

Pour corser un peu le problème, et donner un caractère de plus grande généralité à notre étude, nous avons envisagé des jeux de bien public un peu spéciaux, dits avec seuil. Dans le contexte de création de bien public, cela signifie que si le niveau des contributions est en dessous d’une certaine valeur, le bien public n’est pas créé. Dans notre expérience, nous avons défini différents niveaux de seuil, et si le seuil était atteint, le bien public était créé à hauteur de la somme des contributions atteinte par les individus. Si par contre le seuil n’était pas atteint, les contributions étaient perdues pour les sujets. Cela signifie que si, par exemple, le seuil défini pour créer le bien public est de 60 unités, et que sur les quatre participants du groupe, l’un a investi la totalité de sa dotation en ressources (20 unités) et que les trois autres ont investi ensemble moins de quarante unités, alors le premier obtient un gain égal à zéro.

Dans le contexte de préservation, cela signifie que, au début de la période de jeu, la totalité des dotations des joueurs est placée dans le pot commun (soit 80 unités, puisque chacun des quatre joueurs dispose de 20 unités de droit de retrait), et ceux-ci peuvent exercer un droit de retrait d’au maximum vingt unités chacun. Chaque unité retirée par un joueur lui donne 1 point. Chaque unité restant dans le pot commun, pour peu que le seuil de préservation ne soit pas dépassé, donne 0.4 point à chaque participant, soit 1.6 point pour l’ensemble du groupe de 4 personnes. Par exemple, si le seuil pour lequel le bien public est préservé est de 60 unités, cela signifie que si, par exemple, deux participants sur le groupe de 4 décident de retirer chacun 20 unités et que les deux autres ne retirent rien du tout, le bien public est totalement détruit. Ceux qui ont retiré gagnent 20 points et ceux qui n’ont rien retiré gagnent zéro point.

L’intérêt d’introduire des seuils est double. D’abord, cela correspond plus à la réalité de la plupart des biens publics qui nous entourent, dans la mesure où la quantité de bien public créée par les efforts d’individus au sein d’une collectivité n’est sans doute pas de nature linéaire.Si la collectivité ne fait pas un montant minimum d’effort, le bien public n’est pas réalisé. Par ailleurs, cela modifie la nature des équilibres théoriques de contribution au bien public. Dans le jeu de contribution au bien public sans seuil, l’équilibre en stratégies dominantes est un équilibre de free riding, dans lequel les participants devraient contribuer zéro au bien (ou retirer la totalité de leurs droits). Dans les jeux de contribution au bien public avec seuil, on est en présence de jeux de coordination, dans lesquels les équilibres sont multiples : l’équilibre de free riding existe toujours, mais il existe également de nombreux équilibres de Nash dans lesquels la somme des contributions des joueurs est exactement égale au seuil de création défini (ou, dans le contexte de préservation, la somme des retraits à l’équilibre de Nash est égale au seuil de préservation). Quel équilibre sera au final sélectionné par les joueurs ?
L’équilibre de free riding ou un des équilibres permettant au bien public d’exister ? L’intérêt de l’économie expérimentale est précisément d’établir des résultats qui permettent de faire une idée de la situation qui sera finalement sélectionnée concrètement par le groupe d’individus.

Dans l’expérience que nous avons menée, et qui a eu recours à un peu moins de 400 participants, nous avons mis en œuvre les deux contextes (création vs préservation du bien public) et ce pour quatre niveaux de seuil de bien public (zéro, 28, 60 et 80). Les résultats sont nombreux mais, pour l’essentiel, et à notre grande surprise il faut bien le dire, il s’avère que le résultat d’Andreoni est robuste : les niveaux de coopération sont plus élevés dans le cas d’une création de bien public que dans le cas de la préservation de celui-ci. Le graphique ci-dessous résume brièvement le principal résultat. Plus le niveau de seuil pour le bien public est élevé, plus le niveau de coopération au sein du groupe (la hauteur des barres matérialisant le total des contributions au sein de chaque groupe en moyenne) est élevé, et ceci est vrai dans les deux contextes (création en bleu et préservation en rouge), bien que pour le niveau de seuil maximal (80), les niveaux de coopération soient plus faibles que pour le niveau de seuil immédiatement inférieur. Toutefois, assez nettement, l’écart relatif entre les niveaux de coopération dans les deux contextes est d’autant plus fort que le seuil matérialisant la création ou le maintien du bien public est élevé.

source : Bougherara, Denant-Boemont & Masclet, 2010.

Au-delà de ce résultat qui met en évidence la solidité des résultats expérimentaux concernant les comportements de contribution au bien public, un résultat intéressant et que je laisse à ta sagacité, lecteur, est le suivant. Il semble que, contrairement à ce que l’on observe pour les biens privés, il n’existe pas de de biais de statu quo pour les biens publics. Le fait que le bien public préexiste déjà ne garantit en rien que les individus vont avoir une tendance plus forte à le préserver que la tendance qu’ils ont à créer d’autres biens publics.

Etonnant, non ?